Night Hour

Combinations and Permutations Using Deno

Study hard what interests you the most in the most undisciplined, irreverent and original manner possible. , Richard Feynmann


14 Nov 2020

Introduction

Data structures and algorithms are an important topic in Computer Science and programming. Many of our digital systems rely on these concepts to perform tasks efficiently, within time and resource constraints. Many technology people have studied this stuff at school or through their own self learning. Concepts and skills need refreshers to keep it alive and sharp.

This article runs through combination and permutation algorithm using Deno and typescript. Combination and permutation are similar concept and recursion can be used to solve them.

Design and Approach

Permutation is the number of ways that items can be combined together, order is important. These items are taken from a set of things. For example, we have 20 technical books at home, and the desk shelf only have slots for 5. What are the total number of ways that we can arrange 5 books on our shelf ? What are the possible permutations ?

We can do this manually, taking the books one by one, arranging them on the shelf and noting down the arrangement. Alternatively, we can use maths to calculate the number of permutations, or we can use a programming language and write a program for this.

Permutation is related to combination. It is the superset from which combinations can be derived. Combination does not consider order, so "AB" is the same as "BA". The same program that solves for permutation can be used to obtain combinations as well, by removing duplicate items that contain the same elements but in different order.

A recursive function can be used to generate all possible permutations for a list of items. Recursion works by calling itself with a subset of the original input. For the book shelf example, we can do it in a manual way systematically.

For the 1st slot, there are 20 books available. We can pick the first book and place it in the first slot out of 5. Then we repeat for the second slot. However, this time there are 19 books left (input reduced) and 4 slots available. We repeat for the third, fourth and fifth slots. This gives us a single way of arrangement.

To find other ways of arrangement, we have to be systematic. We can leave the first four slots with their respective books in place and change only the book for the 5th slot. There are 16 books available for the 5 so we keep swapping until we have tried all 16. Then we go back to the 4th slot, there are 17 books available, we have already tried one while changing the 5th slot previously. So we repeat here as well, swapping out the book and putting another one in. For this new book that is on the 4th slot, we can also have 16 different books on the 5th slot. So we go down to the 5th slot and again swapping it 16 times.

Such a systematic process can be repeated, backing up from the 5th slot, to the 4th slot, diving in againt to 5th slot etc... until we reach slot 1. This is actually a recursive algorithm.

Implementation

We will use deno and typescript to implement a combination and permutation generation program. Instead of books, the input is an array of integers or numbers. To keep things, we can start with small inputs. For example, an array of 4 integers and we want to get the possible permutations for 3 integers (The number of slots is 3).

The following is an integer array of numbers that we can use to generate the combinations or permutations.

1
2

/* Array of 4 numbers */
let arr: number[]  = [0,1,2,3];

We define a singlely linked list class, that we called ArrayList. This is to keep the results of all possible combinations of 3. The 3 integers are stored in an array. The following shows the ArrayList class.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

/* Define an ArrayList to store all the combinations of arrays */
class ArrayList {
    combination: number[] = [];
    next: (ArrayList | null) = null;

    constructor(num?: number) 
    {
        if(num !== undefined)
        {
            this.combination.push(num);
        }
       
    }
} 

A constructor is included in the ArrayList. This is to make it convenient to create an ArrayList with a single number in its combination array.

ArrayList is a linked list. ArrayList objects can be linked up one after another. We create a helper function to add a new ArrayList object to the end of an existing ArrayList.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/* Helper function to add to end of another ArrayList */
function addItem(dest: (ArrayList|null), new_list_item: (ArrayList|null)):(ArrayList|null)
{
    if(new_list_item === null)
    {
        return null;
    }

    /* dest is empty */
    if(dest === null)
    {
        dest = new_list_item;
        return dest;
    }

    /* append to end of dest */
    let tmp = dest;
    while(tmp.next)
    {
        tmp = tmp.next; 
    }

    tmp.next = new_list_item;
    return dest;
}

We define another helper function to print out all the combinations in a linked list of ArrayList.

1
2
3
4
5
6
7
8
9

/* Helper function prints the listing of combinations */
function printlist(list:(ArrayList|null))
{
    while(list)
    {
        console.log(list.combination);
        list = list.next;
    }
}

The following is the recursive function, createSubCombin() that does all the magic.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

/* 
   Recursive function to process each position 
   Takes a positive number that indicates the positions available.
   Takes an array of digits as total number of items to generate combination.
   Returns the an ArrayList that contains all possible combinations or permutations

   When the number of positions is equal to the number of items. It is a permutation. 

*/
function createSubCombin(position:number, digits:number[]):(ArrayList|null) {
    
    /* check for error inputs */
    if(digits.length === 0 || position <=0 || position > digits.length)
    {
        return null;
    }

    let ret:(ArrayList|null) = null;

    /* last position, condition to end recursive */
    if(position === 1)
    { 
        for(let i=0;i<digits.length;i++)
        {
            ret = addItem(ret, new ArrayList(digits[i]));
            
        }
       
        return ret;
    }    


   
   for(let i=0 ; i<digits.length; i++)
   {

        let current_digit = digits[i]; 
        let remain_digits:number[];
        if(i===0) { 
            remain_digits = digits.slice(i + 1);
        }
        else
        {
            remain_digits = (digits.slice(i+1)).concat(digits.slice(0, i));
        }
        
        let subresult = createSubCombin(position -1, remain_digits);

        let tmp = subresult;
        while(tmp != null)
        {
            tmp.combination.unshift(current_digit);
            tmp = tmp.next;
        }

        ret=addItem(ret, subresult);

   }

   return ret;
  
}

The function takes in 2 parameters. A position and an array of available digits or numbers for that position. The recursion ends when it is in the last position. It returns an ArrayList of all the available digits at the last position. Think of the 5th slot in our book shelf example and the 16 available books for the slot.

The is a main loop that will loop through all the available digits or numbers for a particular position that createSubCombin() function is called for. For each available digit, it will first save the digit (needed for merging the result), then it prepares a new reduced input for calling createSubCombin() at the next position.

When it receives the ArrayList result from createSubCombin(), it merges the current digit with the result. The current digit is placed at the beginning of the combination array for each ArrayList. It then adds this result to the ArrayList ret. ret is the ArrayList holding all the results for a particular position.

When the main loop completes for all the available digits at a position, ret is returned.

The ABC position thinking

A useful way to think of how this recursion works is to treat the 3 integer positions as ABC. First we hold A. There are BC left. So we call the recursive function again for B. A detail to note is that the available digits for A is [0,1,2,3], our initial array. When calling for B, this array needs to be reduced by 1, since one of the digit is taken by A. The available digits for B will be [1,2,3] if we select 0 for A. It will be [0,2,3] if we select 1 for A, it will be [0,1,3] if we select 2 for A, and it will be [0,1,2] if we select 3 for A.

At B, we hold B. There is only C left (the last position). The available digits for C will be [2,3] if we hold 1 for B and 0 is already held by A. If we hold 2 for B and 0 is already held by A, the available digits for C will be [1,3]. It will be [1,2] if we hold 3 for B and 0 is already held by A and so on...

At C, it is the last position. When it receives an input of [2,3], it simply returns a linked list of ArrayList, the first one containing 2 and the second containing 3.

When B holding 1 got its result of ArrayList containing 2 linked items (2 and 3), it appends 1 to the front of each value. This creates a ArrayList of 2 linked items with values [1,2] and [1,3]. When these values are eventually returned by B to A holding 0. A will repeat what B has done. Appending 0 to these values. It creates [0,1,2] and [0,1,3]. Note B doesn't return immediately after it got one result from C. B adds the items to ret. It waits for other available digits for B (B holding 2, B holding 3) before returning to A holding 0.

Drawing this process out using pen and paper will help to make it clearer. I find this ABC approach to be quite useful and it is one of the first thing to pop up in mind when I think about combination and permutation.

The following shows the rest of the code, to start off the generation of permutations.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

/* To get 3 number combinations out of an array of 4 elements */
/* Consider the 3 numbers as position A, B, C represented by 3,2,1 respectively */
let combination_position = 3;
let list = createSubCombin(combination_position, arr);
console.log("Number of possible combinations for", combination_position, "out of", arr.length);

if(list !== null)
{
    let tmp:(ArrayList|null) = list;
    let num_combination = 0;
    while(tmp !== null)
    {
        num_combination++;
        tmp = tmp.next; 
    }
    console.log(num_combination);
    printlist(list);
}
else
{
    console.error("An error occurred while trying to generate combinations");
}

The same program can be used to generate combinations by removing duplicates with same elements but in different order.

Play around with the program, starting with some small integer array and positions. It allows us to test the logic of the program and check that it produces the correct results.

The full source code is available at the Github link below.

Running the program

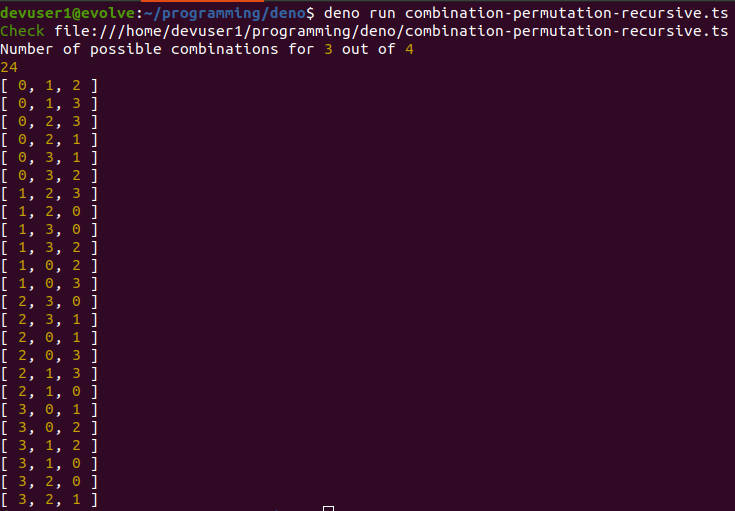
To run the program, we can use the following command.

The screenshot shows the result.

Conclusion and Afterthought

Data structures and algorithms are important parts of Computer Science. It is a useful subject for programmers, software developers, security engineers, database administrators, systems/network administers and other tech professionals to study and learn about.

We often forgot about the algorithms and data structures that we have learnt over time. It is necessary to have refreshers to sharpen our skills and refresh our knowledge of the topic.