Farmer Wolf Cabbage Sheep River Crossing Puzzle
An expert is a person who has made all the mistakes that can be made in a very narrow field
, Niels Bohr
29 May 2017
Introduction
Farmer, wolf, cabbage, sheep is a famous river crossing puzzle. The puzzle goes like this, a farmer wants to move a wolf, cabbage and sheep across a river. The farmer has only a small boat that can sit himself and one passenger. The wolf will eat the sheep if the farmer is not around. The sheep will eat the cabbage if the farmer is not around. How can the farmer ferry all of them across the river ?
The puzzle can be treated as a graph search problem and be solved using either breadth first search or depth first search. This article shows how to build a simple java application that solves this.
Design and Approach
The river crossing puzzle can be viewed as a sequences of states. In the initial state, the farmer, wolf, cabbage and sheep are on one bank of the river (say left side) and the opposite river bank (right) is empty. From this initial state, there are a possible number of moves that the the farmer can take to transition to the next state. For example, the farmer can row himself and the wolf across. This creates a new state where the cabbage and sheep are together on one side of the river, while the farmer and wolf are on the other side. Based on the earlier rules and constraints, the sheep will eat the cabbage; and the farmer fails in his task to bring everything across the river. Therefore moving the farmer and wolf lead to a state that cannot be allowed. Other moves such as, farmer together with cabbage, farmer alone, farmer with sheep can be considered in turn.
When a new state that is allowable is created, additional moves from this state can then be considered and so on, until the solution is reached; or no other moves leading to an allowable new state is possible. The solution is a state where the farmer, wolf, cabbage and sheep are all on the opposite bank of the river from where they started. The following diagram illustrates the state transitions.
Notice that a move that transits to a repeated state that has already occurred in its parent path is not allowed. This is to prevent an endless loop of repetitions.
Breadth First and Depth First Search
The state space described above can be generated by breadth first search or depth first search algorithm. In breadth first search, the parent state is explored, followed by the next level consisting of its children and then the next level of its grand children and so on ... It goes level by level, exploring all the states at a particular level before proceeding to the next level. The number of possible moves/transitions from each state to a new state is the branching factor. In this puzzle, it is 4 or less moves (F, FW, FS, FC). Breadth first search has a large memory space requirements and time complexity of O(b d +1) where b is branching factor and d is depth or level.
Depth first search on the other hand, goes down the deepest path until a solution is found or no possible moves can be made. It then backtracks up and try the next path. This process continues until the entire search space has been explored. Depth first search requires less memory space than breadth first and it has a time complexity of O(bd) where b is branching factor and d is the depth of the search tree.
An enhanced version of depth first search is iterative deepening depth first search. This techniques utilizes depth first search but with an increaing depth limit for each iteration. For example, in the first iteration, it expands using depth first search using a depth limit of 1, if no solution found, it goes into the next iteration and uses a depth limit of 2 and so on ... until solutions are found or the maximum allowable depth limit is reached.
Implementation
The application consists of a single FarmerWolfCabbageSheep class file with two inner classes, State and Node. The State class represents that possible states of the puzzle at any one time. For example, the initial state where the farmer, wolf, cabbage and sheep are all on one side of the river. The Node class are used for constructing the state graph containing the various states arising from the moves/transitions.The following snippet shows the State inner class. The method isAllow() checks if the state is an allowable state where the constraints and rules are met. The isSolution() method checks if it is a solution state. The transits() method creates a new state based on the move.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 | /**
* Private Inner State class to represent a state A state consists of the
* occupants (farmer, wolf, sheep, cabbage) on the left and right bank of
* the river One of the river bank (left or right) is where the farmer is
* located and from here the farmer can cross the river to the opposite bank
* optionally bringing along another occupant(wolf , sheep, cabbage)
*
* It is assumed that the initial state is
*
* left bank: farmer(F), wolf(W), cabbage(C), sheep(S) right bank:
*
* All occupants including the farmer is on the left bank and the right bank
* is empty. The farmer will attempt to move everyone to the right bank
* through a sequence of crossings subjected to the constraints in the
* puzzle. Farmer can at most move one more occupant besides
* himself/herself. Wolf , sheep cannot be together without farmer. Cabbage,
* sheep cannot be together without farmer. The solution state will be
*
* left bank: right bank: farmer (F), wolf(W), cabbage(C), sheep(S)
*
* The left bank is empty and all the occupants farmer, wolf, cabbage and
* sheep are on the right bank.
*
*/
private class State
{
private String bank; // The active bank where the farmer is currently
// located
private TreeSet<String> left, right; // left and right bank with its
// occupants.
public State(String bank, TreeSet<String> left, TreeSet<String> right)
{
this.bank = bank;
this.left = left;
this.right = right;
}
/**
* Takes a TreeSet<String> that contains the occupants in a river bank
* (left or right) and check whether the puzzle constraints Wolf , sheep
* cannot be together without farmer Cabbage, sheep cannot be together
* without farmer are met.
*
* @param b An TreeSet<String> representing the river bank with its
* occupants
* @return true if puzzle constraints are met, false otherwise.
*/
private boolean checkAllowBank(TreeSet<String> b)
{
// Wolf and Sheep together without Farmer
if (b.contains("W") && b.contains("S") && (b.contains("F") == false))
return false;
// Sheep and Cabbage together without Farmer
if (b.contains("S") && b.contains("C") && (b.contains("F") == false))
return false;
return true;
}
/**
* Public method to check if a State meets the puzzle constraints.
* Disallow states are those that doesn't meet the puzzle constraints.
*
* @return true if a State is allowed, false otherwise.
*/
public boolean isAllow()
{
if (checkAllowBank(left) && checkAllowBank(right))
return true;
else
return false;
}
/**
* Check for the solution state where the puzzle is solved.
*
* @return true if it is solution state, false otherwise.
*/
public boolean isSolution()
{
if (left.isEmpty() && right.contains("W") && right.contains("S") && right.contains("C")
&& right.contains("F"))
return true;
else
return false;
}
/**
* Transit to a new child State based on the move.
*
* @param move ,Parameter containing the moves (F, FW, FS, FC) to
* transit to a new child State.
* @return State , a new child State based on the transition or null if
* the move is not allowed.
*/
public State transits(String move)
{
String nbank;
TreeSet<String> nleft = new TreeSet<String>();
TreeSet<String> nright = new TreeSet<String>();
if (bank.equalsIgnoreCase("left"))
nbank = "right";
else
nbank = "left";
copylist(right, nright);
copylist(left, nleft);
for (int i = 0; i < move.length(); i++)
{
String item = move.substring(i, i + 1);
if (bank.equalsIgnoreCase("left"))
{
if (nleft.remove(item))
nright.add(item);
else
return null; // return null if the move contains
// occupants that are not present.
}
else
{
if (nright.remove(item))
nleft.add(item);
else
return null; // return null if the move contains
// occupants that are not present.
}
}
return new State(nbank, nleft, nright);
}
/**
* Method to duplicate/copy a representation of the river bank and its
* occupants from source to destination.
*/
private void copylist(TreeSet<String> src, TreeSet<String> dst)
{
for (String e : src)
dst.add(e);
}
/**
* Compares current state with a specific state
*
* @param s The State s to compare with
* @return true if the current and specified state are the same, false
* otherwise
*/
public boolean compare(State s)
{
TreeSet<String> tmp;
if (!s.getBank().equalsIgnoreCase(bank))
return false;
tmp = s.getLeft();
for (String e : left)
{
if (!tmp.contains(e))
return false;
}
tmp = s.getRight();
for (String e : right)
{
if (!tmp.contains(e))
return false;
}
return true;
}
public String getBank()
{
return bank;
}
public TreeSet<String> getLeft()
{
return left;
}
public TreeSet<String> getRight()
{
return right;
}
@Override
public String toString()
{
StringBuffer ret = new StringBuffer();
ret.append("{L:");
for (String e : left)
ret.append(e);
ret.append(" ");
ret.append("R:");
for (String e : right)
ret.append(e);
ret.append("}");
return ret.toString();
}
}
|
The following shows the code snippet for the Node inner class. It holds a class variable parent that links to its parent node. There is a ArrayList variable holding its children, a variable that holds the State. The isAncestor() method checks whether the current state of the Node has occurred previously along its parent path. To prevent an endless repetitions loop, repeated states along a path is disallowed.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | /**
* Private Inner class Node for constructing the State graph
*/
private class Node
{
public Node parent; // Parent of the node
public State data; // State of the node
public ArrayList<Node> adjlist; // Children of the node
public int level; // Depth of the node
public String move; // The move (transition) that creates the current
// node state.
public Node(State data)
{
parent = null;
this.data = data;
adjlist = new ArrayList<Node>();
level = 0;
move = "";
}
/**
* Checks if a Node that has the same State is an ancestor of the
* current Node.
*
* @return true if a an ancestor node has the same state, false
* otherwise
*/
public boolean isAncestor()
{
Node n = parent;
boolean ret = false;
while (n != null)
{
if (data.compare(n.data))
{
ret = true;
break;
}
n = n.parent;
}
return ret;
}
}
|
The startBreadthFirstSearch() method in the outer class FarmerWolfCabbageSheep, generates the state space graph using breadth first search. It starts off with a queue containing the initial root node. It process the root, removes it from the queue and adds any valid child nodes into the queue for further processing. When a solution is found, it is added to an ArrayList member variable , solutions. The following shows the code snippet.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | /**
* Method to start the creation of the state graph using breadth first
* search, transiting to allowable states
*/
public void startBreadthFirstSearch()
{
solutions = new ArrayList<Node>(); // Initialize solutions to zero
TreeSet<String> left = new TreeSet<String>();
left.add("W");
left.add("S");
left.add("C");
left.add("F");
State inits = new State("left", left, new TreeSet<String>());
root = new Node(inits);
root.level = 0;
queue.add(root);
while (!queue.isEmpty())
{
Node n = queue.remove(0);
System.out.println("Processing Level " + n.level + " " + n.data);
for (String m : moves)
{
State s = n.data.transits(m);
if (s != null && s.isAllow()) // Check if it is allowable state
{
Node child = new Node(s);
child.parent = n;
child.level = n.level + 1;
child.move = m + " moves " + child.data.getBank();
// Check that a node doesn't occur already as ancestor to
// prevent cycle in the graph
if (!child.isAncestor())
{
n.adjlist.add(child);
if (child.data.isSolution() == false)
{
queue.add(child);
System.out.println("Adding state " + child.data);
}
else
{
solutions.add(child);
System.out.println("Found solution " + child.data);
}
}
}
}
}
}
|
The depth first implementation consists of two methods. The startDepthFirstSearch() method starts the iterative deepening depth first search. It calls the startDFS() method which implements depth first search with a depth limit using recursion. The depth first implementation is independent of the earlier breadth first search method. Both the depth first and breadth first implementation generate the state graph and find solutions independently. The state graph generated and the solutions found though should be the same. The following snippet shows the depth first implementation.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 | /**
* Method to start the creation of the state graph using iterative depth
* first search
*/
public void startDepthFirstSearch()
{
int dlimit = 1; // Maximum depth limit
solutions = new ArrayList<Node>(); // Initialize solutions to zero
while (solutions.size() == 0 && dlimit <= 10)
{
TreeSet<String> left = new TreeSet<String>();
left.add("W");
left.add("S");
left.add("C");
left.add("F");
State inits = new State("left", left, new TreeSet<String>());
root = new Node(inits);
root.level = 0;
System.out.println("Starting iterative DFS with depth: " + dlimit);
startDFS(dlimit, root);
dlimit++;
}
}
/**
* Recursive Method to create the state graph using Depth first search (DFS)
*
* @param depth limit of the DFS search
* @param Node that holds current state
*/
public void startDFS(int depth, Node r)
{
if (depth == 0)
{
System.out.println("Maximum depth limit");
return;
}
System.out.println("Processing Level " + r.level + " " + r.data);
for (String m : moves)
{
State s = r.data.transits(m);
if (s != null && s.isAllow()) // Check if it is allowable state
{
Node child = new Node(s);
child.parent = r;
child.level = r.level + 1;
child.move = m + " moves " + child.data.getBank();
if (!child.isAncestor()) // Check that the node doesn't occur
// already as an ancestor
{
r.adjlist.add(child);
if (child.data.isSolution())
{// Found a solution
solutions.add(child);
System.out.println("Found solution " + child.data);
return;
}
else
{// Recursive call
startDFS(depth - 1, child);
}
}
}
}
// No valid states
return;
}
|
The following snippet shows the main method of the FarmerWolfCabbageSheep class. It creates a new FarmerWolfCabbageSheep object and finds the solutions to the river crossing puzzle using both the breadth first and depth first implementation. The full source code for the class is available at the Github link at the bottom of the article.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | public static void main(String[] args)
{
System.out.println("Solving Wolf, Sheep, Cabbage, Farmer, River Crossing Puzzle\n");
FarmerWolfCabbageSheep obj = new FarmerWolfCabbageSheep();
System.out.println("Creating State Graph using Breadth First Search");
obj.startBreadthFirstSearch();
System.out.println("\n\nState Graph in Breadth first order");
obj.printBFSGraph();
System.out.println("\n\n");
System.out.println("Solutions to the River Crossing Puzzle BFS");
obj.printSolution();
System.out.println("\n\nCreating State Graph using Iterative Depth First Search");
obj.startDepthFirstSearch();
System.out.println("\n\nState Graph in Breadth first order");
obj.printBFSGraph();
System.out.println("\n\n");
System.out.println("Solutions to the River Crossing Puzzle Iterative DFS");
obj.printSolution();
}
|
Results of Running the Application
To solve the farmer, wolf, cabbage, sheep, river crossing puzzle, compile the java class and run it.
java FarmerWolfCabbageSheep
The application will solve the puzzle using breadth first state and then solve it again using iterative deepening depth first search. The solutions and the state graph generated using both methods will be printed out, one after the other. The following screenshot shows the result from the breadth first search, the result from the iterative depth first search is further down and not shown here.
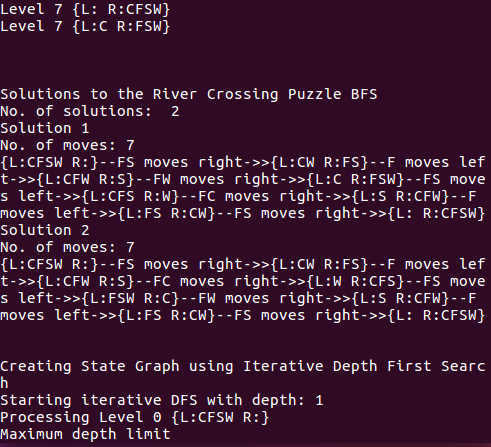
There are a total of 2 solutions to the puzzle. The results show the states represented by curly bracket, the L: indicate left side of the river, while R: indicate right side of the river. C stands for cabbage, S for sheep, F for farmer and W for wolf. The following shows the representation of the initial state, where the cabbage, sheep, farmer and wolf are all on the left side of the river.
A state transits to another through a move. Move are represented by -- Members move right->> or -- Members move left->> , where Members are combinations of F, C, S or W. The following shows an example of farmer and sheep moving to the right side of the river.
The two possible solutions involve a total of 7 moves. The following shows the 2 solutions. Both the breadth first and depth first method will return the same set of solutions.
No. of moves: 7
{L:CFSW R:}--FS moves right->>{L:CW R:FS}--F moves left->>{L:CFW R:S}--FW moves right->>{L:C R:FSW}--FS moves left->>{L:CFS R:W}--FC moves right->>{L:S R:CFW}--F moves left->>{L:FS R:CW}--FS moves right->>{L: R:CFSW}
Solution 2
No. of moves: 7
{L:CFSW R:}--FS moves right->>{L:CW R:FS}--F moves left->>{L:CFW R:S}--FC moves right->>{L:W R:CFS}--FS moves left->>{L:FSW R:C}--FW moves right->>{L:S R:CFW}--F moves left->>{L:FS R:CW}--FS moves right->>{L: R:CFSW}
In the transition listing shown above, solution 1 is as follows:
- Farmer rows Sheep to right river bank, leaving wolf and cabbage on the left bank.
- Farmer comes back alone. Sheep is on right bank, wolf and cabbage on left bank.
- Farmer rows wolf across to the right river bank where sheep is waiting, leaving cabbage on the left bank.
- Farmer rows sheep back to the left river bank, leaving wolf alone in right bank.
- Farmer rows cabbage to the right river bank, leaving sheep alone on the left bank.
- Farmer comes back alone. Sheep is on left bank, wolf and cabbage on right bank.
- Farmer rows sheep to the right bank where wolf and cabbage are waiting. All of them are now on the right bank.
The alternative solution 2 is as follows:
- Farmer rows Sheep to right river bank, leaving wolf and cabbage on the left bank.
- Farmer comes back alone. Sheep is on right bank, wolf and cabbage on left bank.
- Farmer rows cabbage across to the right bank where sheep is waiting, leaving wolf on the left bank.
- Farmer rows sheep back to the left bank, leaving cabbage alone in the right bank.
- Farmer rows wolf to the right bank, leaving sheep alone on the left bank.
- Farmer comes back alone. Sheep is on left bank, wolf and cabbage on right bank.
- Farmer rows sheep to the right bank where wolf and cabbage are waiting. All of them are now on the right bank.
Conclusion and Afterthought
Graph search such as breadth first or depth first search are algorithms often used in artificial intelligence to solve problems, such as playing games, path finding etc... The river crossing puzzle is an easy and popular way to learn and apply such graph traversal algorithms.
The full source code for the FarmerWolfCabbageSheep.java is available at the following Github link.
https://github.com/ngchianglin/FarmerWolfSheepCabbageRiverCrossing
If you have any feedback, comments, corrections or suggestions to improve this article. You can reach me via the contact/feedback link at the bottom of the page.
Article last updated on Dec 2017.